Игри на късмета: Научете за печалбите и вариативността
Принципите, описани в тази статия, могат да се прилагат почти във всяка игра на късмета, в която играча играе срещу казиното. С други думи, всички игри, в които казиното събира залози и изплаща потенциални печалби. Най-известните такива игри са слот машини, рулетка, блекджек и бакара, но има и много други.
Повечето от вас навярно знаят, че тези игри са настроени да дават определено преимущество на казиното в дългосрочен план. В противен случай собствениците на казиното щяха да губят пари от тях. Това предимство е познато като предимство на казиното.
Предимството на казиното се определя от правилата на всяка игра, както и от правилата за изплащане в случай на победа. Ако тези правила се прилагат в много, много рундове (понякога дори стотици и хиляди пъти), собствениците на казиното могат да са сигурни, че сумата на събраните залози ще превиши сумата на изплатените печалби. Статистиките работят в полза на казиното в дългосрочен план.
Въпреки че в дългосрочен план статистиките са срещу вас, често може да дойдете в казиното, да играете, да спечелите и да си тръгнете с печалба. Основната причина е, че вашето посещение в казиното представлява само няколко от десетки или стотици рунда в играта. В този случай, статистиките нямат достатъчно време да се доближат (проявят). Изходът от вашето посещение в казиното се определя повече от шанса (или от късмета, ако желаете). Това е точно този шанс, който помага на играчите с късмет да спечелят и да победят статистическото предимство на казиното, въпреки че това е само в краткосрочен план.
За да увеличите шансовете си да "победите статистиките" е изключително важно да знаете двете важни характерни черти на всяка игра – коефициент на изплащане и вариативност. Точно върху това ще се съсредоточим в тази статия.
Ще обясним за:
- Коефициент на изплащане (възвръщаемост)
- Вариативност (волатилност)
- Възвръщаемост на система за залагане
- Заключения
Игри на късмета и коефициент на изплащане (възвръщаемост)
Коефициентът на изплащане (познат още като очаквана печалба, процент на печалба или възвръщаемост) в игра на късмета е дългосрочният статистически коефициент на общо спечелените пари, разделени на общо заложените пари. Противоположното на коефициента на изплащане е предимството на казиното. Предимството на казиното се калкулира като 100% минус коефициента на изплащане. Ако коефициентът на изплащане е 95%, то тогава предимството на казиното е 100% - 95% = 5%.
Нека разгледаме подробно коефициентите на изплащане в по-популярните игри на късмета.
Коефициент на изплащане на рулетка
В европейската рулетка вероятността за печалба при залагане на черен цвят е 18 (# броят на черните числа) разделени на 37 (# броят на всички числа, не забравяйте нулата). Печалбата е 2 пъти залога.
Коефициентът на изплащане на рулетката в случая е 2 * 18 / 37 = 0.973 = 97.3%. Следователно предимството на казиното е 100% – 97.3% = 2.7%. Играта на рулетка има еднаква възвръщаемост за всички видове залози (цветове, числа и т.н.)
Възвръщаемост в блекджек
Тъй като правилата в блекджек могат да се различават в различните казина, то очевидно това важи и за възвръщаемостта. Но в общи линии игра на блекджек, играна от играч, който използва основната блекджек стратегия предоставя очаквана възвръщаемост от около 99.5%.
При блекджек на живо и онлайн очакваната възвръщаемост се променя,тъй като крупието раздава карти от тестето. Възвръщаемостта в този случай е между 95% и 102%, в зависимост кои карти са останали в "обувката". Това се използва от броячите на карти – играчи, които прогнозират действителната възвръщаемост на блекджек тестето и се опитват да правят големи залози, ако възвръщаемостта е над 100%, с цел дългосрочна печалба. От своя страна казината имат средства, чрез които да открият такива броячи на карти и да не им позволят да продължат да играят.
Коефициент на изплащане при слот машините
Възвръщаемостта на слотовете обикновено е между 92% и 99%. Коефициентът на изплащане при слот машините се определя от символите на виртуалните барабани, от таблицата с печалби и от други специфични правила, приложими към всяка конкретна игра.
Вариативност (волатилност) на игрите на късмета
За да го кажем просто, вариативността (позната още като волатилност) на играта определя колко често вашата сметка се променя докато играете играта:
- Когато играете игра с ниска вариативност, печелите малки печалби често. В този случай сметката ви се променя доста равномерно, въпреки това, за жалост, обичайно надолу.
- В случай на игра с висока вариативност, губите в голяма част от рундовете, но когато спечелите, печалбата е висока. Постепенните спадове се заменят от време навреме с голяма печалба.
Вариативността на играта може да бъде описана като статистическо разпределение на печалбите. Тъй като те обикновено са пропорционални на размера на залога, ние говорим за разпределение на печалбите, изразено като множител на залога. Когато залагате на цвят в рулетката, всички печалби се изплащат като удвояване на залога. Когато залагате на едно число, всички печалби се изплащат като 36 пъти залога.
Вариативността на слотовете е малко по-сложна. Можете да улучите различни печеливши комбинации и да спечелите много различни множители на залога си. Поради тази причина не е толкова лесно да опишете вариативноста на слота с едно число и доставчиците на игри използват рехави описания като "малка", "средна", и "висока" за техните слот машини.
Вариативността на играта има значително влияние върху шанса да си тръгнете от казиното като победител. Основното правило е "Колкото е по-голяма вариативността, толкова по-добре":
- Първата причина е, че в игра с висока вариативност е по-лесно да се спечели задоволителна сума в един рунд от играта.
- Втората причина е, че повечето рундове завършват със загуба и за това не залагате толкова много от предходните печалби (което има негативно влияние върху възвръщаемостта на системата ви за залагане). С други думи, губите по-бързо.
- Третата причина е, че ако можете да спечелите по-висок множител на залога, можете да залагате по-малко, за да имате шанса да спечелите същата сума. Това намалява общата сума на залозите и следователно намалява дългосрочните загуби.
За пример, нека си представим игра без вариативност и 99% възвръщаемост. В тази игра залог от 1 лев ще спечели 99 стотинки. Изходът от всеки рунд ще е предопределен и печалбата в тази игра ще е невъзможна. Разбира се, никой няма да хареса тази игра, но тя показва факта, че високата възвръщаемост не е всичко, което има значение.
Очаквана възвръщаемост на система за залагане
Много е важно да разберете, че процентът на изплащане изразява очакваната печалба от един рунд в играта. Да предположим, че залагате100 лева на рулетка и печелите 1200 лева. Тогава продължавате да играете и залагате 12 пъти по 100 лева = 1200 лева. Възвръщаемостта трябва да бъде използвана във всеки рунд отделно. Очакваната статистическа печалба на казиното в този случай ще бъде (100 лв. + 1200 лв.) * (100% - 97.3 %) = 1300 лв. * 2.7 % = 35.1 лв.
Имайте предвид, че 97.3% е възвръщаемостта на европейската рулетка. Ако продължите да играете с предходните си печалби, тогава трябва да очаквате да загубите повече от посоченото преди преимущество на казиното в играта. Повечето от играчите поставят залози от техните предходни печалби отново и отново, губейки част от парите си всеки път.
Ако искате да сте по-умен играч трябва да разграничавате възвръщаемостта (която се прилага само към един рунд в играта) и очакваната печалба от системата ви за залагане.
Вашата система за залагане се определя от това как играете през целия си престой в казиното или цялата сесия в онлайн казиното. Това включва избора на игра, нейният вариант и настройки, размер на залозите и решения за това кога да спрете да играете.
Трудно е да си представите възвръщаемостта на система за залагане, имайки предвид само един играч. За това ние винаги правим симулации с поне един милион играчи - за да получим достоверни резултати. Очакваната възвръщаемост на системата за залагане може да бъде определена като съотношение на общите печалби на играчите, които са успели да улучат техните "цели", към нетните загуби на играчите, които не са извадили късмет.
В действителност, ако играчите поставят залози, използвайки техните предишни печалби, те губят повече пари. Възвръщаемостта на лоша система за залози може да падне под 50%. Дори и при блекджек - игра с принципна възвръщаемост от 99.5%. Както ще видите, възвръщаемостта на лоша система за залози е близка до 0%.
Оптималната система за залагане е тази, която има същата възвръщаемост като играта, която играете. За да постигнете това, трябва да избягвате поставянето на залози с парите, които сте спечелили. Теоретично най-лесния начин да постигнете това, е да заложите целия си бюджет в един рунд. След това продължете да залагате докато загубите или спечелите задоволителна сума пари. Рулетката е много добра игра за тази система, тъй като можете да изберете коефициент за залога си.
Нека предположим, че имате 100 лева за игра и би ви удовлетворила крайна сума от 900. Поставянето на залог от 100 лева на квадрат (4 числа) е почти оптималната стратегия в този случай. Вие или ще напуснете казиното с добра сума пари или без 100 лева, но шансовете са равни. Най-големият недостатък на този подход е, че играете в много кратък период от време.
Как вариативността на играта влияе на очакваната печалба на системата за залагане
Сега ще ви демонстрираме една много проста система за залагане. Забележете как вариативността на играта влияе на очакваната печалба на системата за залагане. Представете си двама играчи, всеки от които е дошъл в казиното със 100 лева.
- Играч Х залага 10 лева на число в рулетката.
- Играч Y поставя залог на цвят.
Всеки от тях напуска казиното, ако сметката надхвърли 500 лева или ако загуби всичките си пари. Ние симулирахме действията на двамата играчи един милион пъти, използвайки проста софтуерна програма с генератор на случайни числа.
Играч X си тръгна от казиното като победител в 14.8% от опитите. Средната му "печалба" бе 648 лева и той изигра средно по 16 рунда. Това означава, че възвръщаемостта на системата за залагане е 95.19%.
Играч Y успява да спечели само в 5.15% от опитите си. Неговата система има средна "печалба" от 500 лева и обща възвръщаемост от 21.42%. От друга страна играч Y се наслаждава на по-дълго игрово време – средно 274 рунда.
От този пример ясно може да видите, че вариативността на играта значително влияе на шансовете да си тръгнете от казиното като победител. Коефициентът на изплащане на системата на играч X бе 4.4 пъти по-висок от възвръщаемостта на системата, използвана от играч Y.
Как размерът на залога влияе на възвръщаемостта на системата за залагане.
Печалбите в игрите на късмета обикновено се калкулират, използвайки размера на залога. Следователно общият коефициент на изплащане също е повлиян от размера на залозите. Правилото на палеца е просто: Колкото по-висок е размерът на залозите ви, толкова по-висока (обикновено) е възвръщаемостта на система за залагане. Ние допускаме, че всички други правила и параметри на системата за залагане, включително и паричната сума, остават едни и същи.
Отново ще използваме рулетка, за да демонстрираме ефекта на размера на залога върху резултатите на системата. Играчите отново идват в казиното със 100 лева и си тръгват, ако паричната сума достигне до 0 или превиши 500 лева. Играч X залага 20 лева и играч Y залага 5 лева във всеки рунд на играта. И двамата играчи залагат на цвят (черно или червено).
- След като симулирахме един милион случаи на играч X, ние открихме, че в 10.9% от тях той успя да достигнае до 500 лева. Това означава възвръщаемост от 48.68% и средно 84 изиграни рунда.
- От друга страна, от един милион случаи на играч Y, само в 0.88% имаше печалба (средно 706 рунда, възвръщаемост от 3.55%). Ако играч Y иска да си тръгне от казиното с 500 лева, той трябва да спечели с 80 рунда повече, отколкото загуби. Изглежда, че да имаш такава „поредица" на рулетка се случва доста рядко.
Статистиките са ясни в този случай. Когато поставяте ниски залози на игра с ниска вариативност, може би ще играете по-дълго, но шансовете да спечелите задоволителна сума падат драстично.
Една от противоположните страни на спектъра на вариативността е комбинацията от висока вариативност с високи залози. Играч Z идва в казиното със 100 лева и решава да заложи всичко на рулетка на едно число. Резултатите от симулацията показват как от един милион Z играча, само 2.71% са успели да спечелят. Въпреки това всеки от победителите си тръгва с 3600 лева (възвръщаемост от 97.4%). Всеки един от Z играчите изиграва точно един рунд.
Препоръчаната система за залагане на рулетка
Добрата система за залагане следователно е компромис между коефициента за задоволителна победа и неговия размер, както и престоя в казиното.
Коя система за залагане ще изберете, ако решите да играете в разумен период от време, имайки добри шансове за печалба? Следната таблица показва резултатите от нашите симулации. Променливите са размера на един залог и вида му (цвят/число). Всеки играч започва със 100 лева и си тръгва от казиното с 500 лева или повече (или след като изгуби всичко).
Таблицата съдържа дела на играчи, които са успели да спечелят, средния размер на печалбата им, калкулираната възвращаемост на системата за залагане и средния брой изиграни рундове.
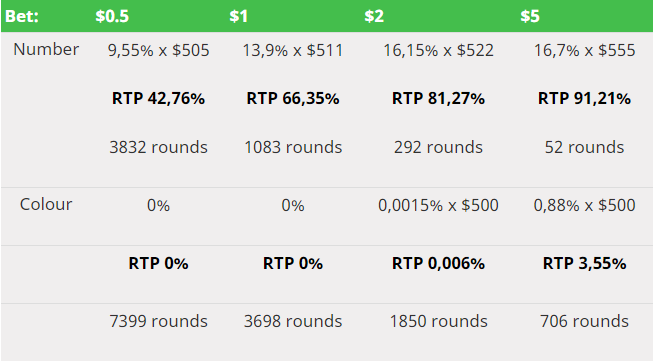
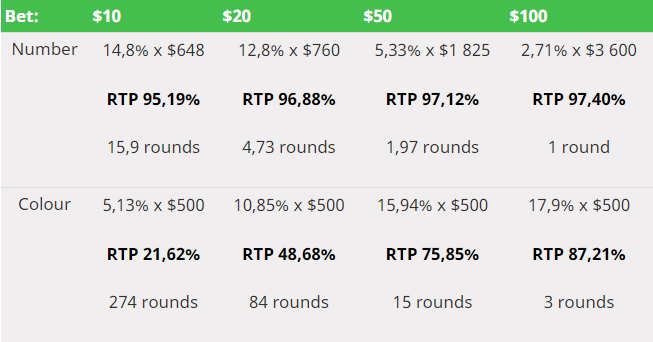
Както можете да видите, много по-високата вариативност на залозите на число лесно може да победи залозите на цвят, които са значително по-големи в размер. В допълнение, вашият престой в казиното ще отнеме повече време. Също така имайте предвид, че когато залагате 2 лева на цвят, шансовете ви да достигнете до 500 лева клонят към нулата. В този случай от един милион опита нямаше дори един успешен.
Ако целта ви е да се забавлявате и да имате добри шансове за победа, ние препоръчваме да изберете играта с възможно най-високата вариативност и да играете с достатъчно малки залози.
В случая с рулетката и бюджета от 100 лева залагането на 2 – 4 лева на късметлийско число изглежда една от най-добрите опции с фиксиран вид и размер на залога.
Заключения
Ето най-важните неща, които да запомните от тази статия:
- Коефициентът на изплащане на игрите на късмета се прилага само когато имате предвид един рунд от играта. Действителната очаквана възвръщаемост ще бъде по-ниска поради повторното залагане на предишните печалби.
- Статистически вие губите на всеки залог. По-малко залози означават по-малка статистическа печалба за казиното.
- Възвръщаемостта навВашата система за залагане зависи от възвръщаемостта на играта, вариативността ѝ, размера на залозите и правилата за това кога да се откажете и кога да продължите да играете.
- Вариативността на играта се определя от размера на потенциалните печалби като множител на залозите. Колкото по-висока е индивидуалната печалба, толкова по-висока е вариативността на играта (считайки фиксирана възвръщаемост).
- Игрите с по-висока вариативност обичайно са по-благоприятни. Предимството на по-висока вариативност може лесно да победи предимството на малко по-високата възвръщаемост.
- Колкото по-висока е вариативността, толкова по-голям е шансът да превърнете малка сума пари в голяма.
- Колкото по-големи са залозите в един рунд, толкова по-голяма е възвръщаемостта на вашата система за залагане, при фиксирана сума за игра.
- Ако играете за забавление, потърсете игри с висока вариативност и поставяйте малки залози. Няколко победи могат да донесат желаната печалба, в противен случай ще загубите целия си бюджет. Имайте предвид, че правите компромис между продължителността на играта ви и възвръщаемостта на системата за залагане.









